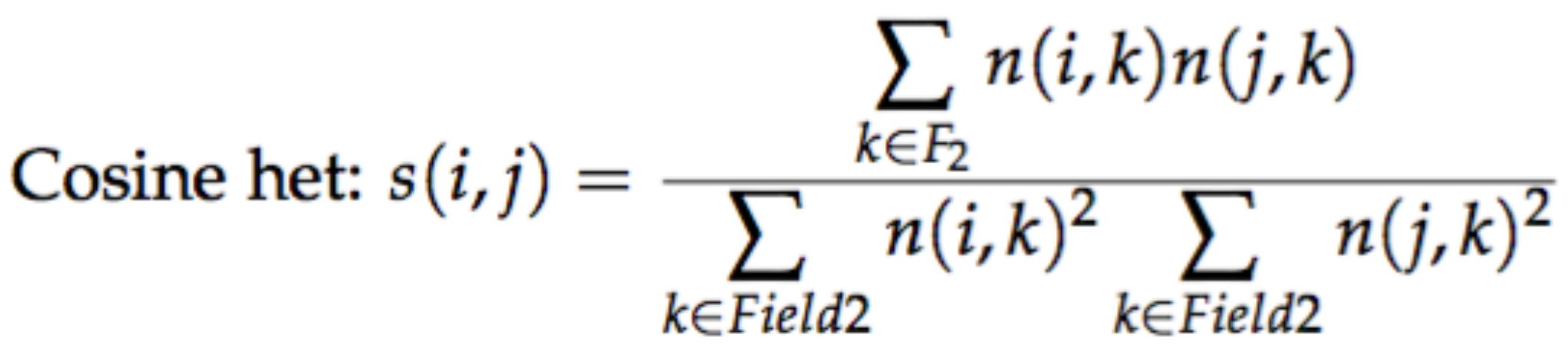n(i, j) is defined as the raw number of cooccurrences between items i and j chosen in two fields F₁ and F₂. In most cases it is simply the number of articles where i and j are jointly present. We will denote n(i) the sum of cooccurrences of item i (sum of rows), n(j) the sum of cooccurrences of item j (sum of columns), and n the sheer sum of all cooccurrences (sum of rows and columns).

 

The expected number of cooccurrences between two items i and j is approximated by:

 

 

Direct similarity measure

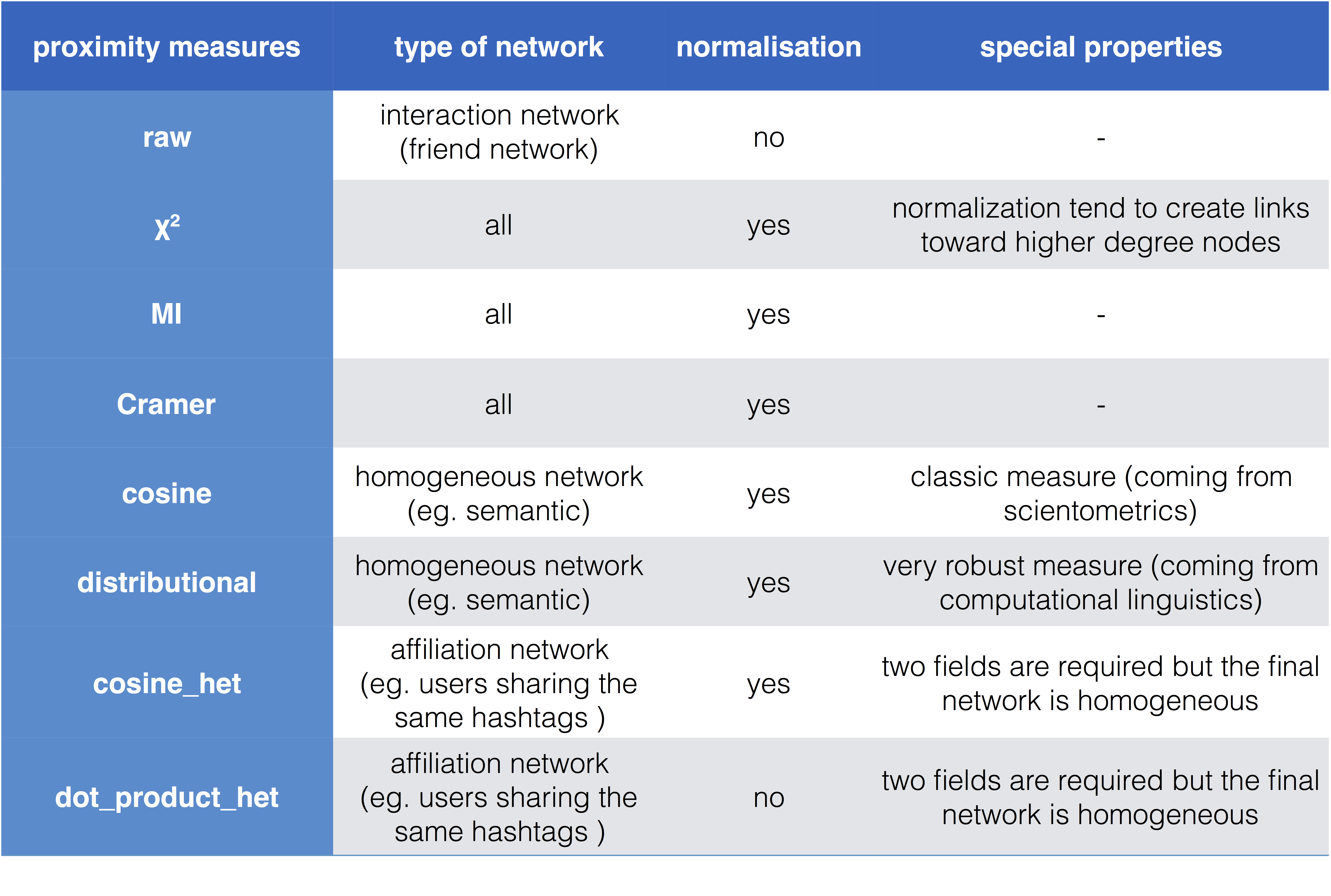
From those variables we use the following equations for the “direct” similarity measures for which entities may belong to the same field or not (homogeneous F₁ = F₂ or heterogenous networks F₁ ≠ F₂):

Raw

 

n(i, j) is defined as the raw number of cooccurrences between items i and j chosen in two fields F₁ and F₂.

Chi2

 

Pearson, K. (1900). On the criterion that a given system of deviation from the probable in the case of a correlated system of variable is such that it can be reasonable, supposed that have arisen from random sampling. Phylosophical Magazine, 50(5), 157–175.

Mutual Information

 

Church, K. W., & Hanks, P. (1989). Word association noms, Mutual Information, and lexicography. In Proceedings of the 27th Annual Conference of the Association for Computational Linguistics (pp. 22–29). Vancouver, British Columbia.

Weeds, J., & Weir, D. (2005). Co-occurrence Retrieval: A Fexible Framework for Lexical Distributional Similarity. Computational Linguistics, 31(4), 339–445.

Cramer

 

Cramer, E. M., & Nicewander, W. A. (1979). Some symmetric, invariant measures of multivariate association. Psychometrika, 44(1), 43–54.

Indirect similarity measure

Cosine and distributional measures are only designed for homoge­neous networks (F₁ = F₂). They are “indirect” measures meaning that the proximity between two different entities i and j depend on their cooccurrences count with any third entity k.

Cosine

 

 

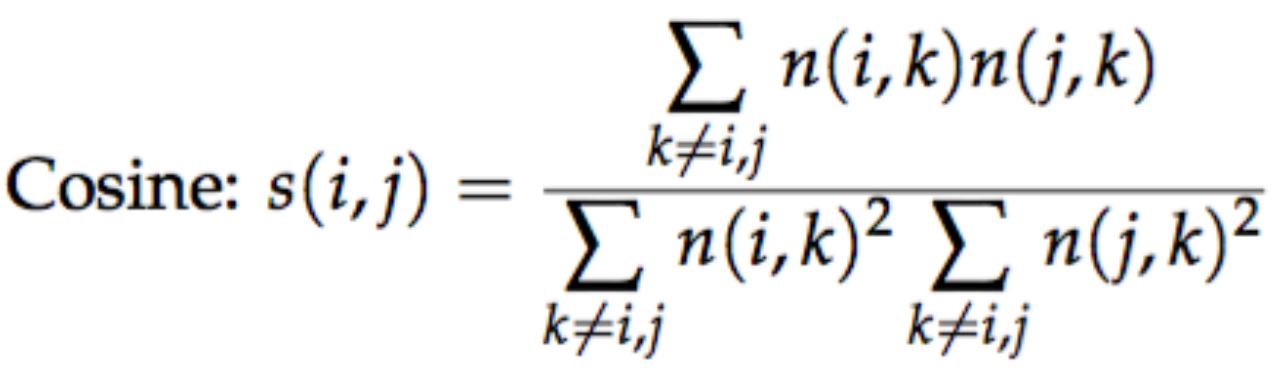
Eck, N. J. Van, & Waltman, L. (2009). How to Normalize Co-Occurrence Data ? An Analysis of Some Well-Known Similarity Measures. Journal of the American Society for Information Science and Technology, 60(8), 1635–1651.

Hamers, L., Hemeryck, Y., Herweyers, G., Janssen, M., Keters, H., Rousseau, R., & Vanhoutte, A. (1989). Similarity measures in scientometric research: The Jaccard index versus Salton’s cosine formula. Information Processing and Management, 25(3), 315–318.

Salton, G., Wong, A., & Yang, C. S. (1975). A Vector Space Model for Automatic Indexing. Magazine Communications of the ACM, 18(11), 613–620.

Distributional

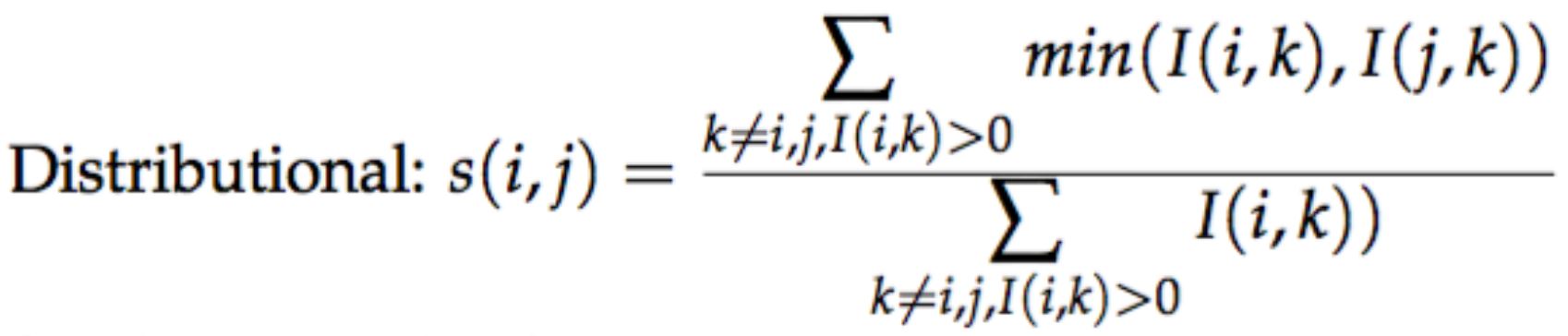
where I stands for the mutual information.

 

Weeds, J., & Weir, D. (2005). Co-occurrence Retrieval: A Fexible Framework for Lexical Distributional Similarity. Computational Linguistics, 31(4), 339–445.

Distributional l-l r

The Distributional l-l r proximity measure is similar than the classic Distributional, with a small distinction:

• Distributional: as shown above, the cooccurrences matrix is based on the Mutual Information between nodes.
• Distributional l-l r: the cooccurrences matrix is based on the Log-Likelihood Ratio between nodes.

The two share the same characteristics: the nodes (e.g. keywords) are close when they play similar roles/functions regarding the contexts in which they appear (e.g. sentences/paragraphs). But the distributional log-likelihood ratio tends to be more respectful to the indirect relations with small frequencies.

Cointet, J.P. (2017). HDR, La cartographie des traces textuelles comme méthodologie d’enquête en sciences sociales, 79.

Affiliation networks: homogenous networks from heterogenous fields

Metrics suffixed by “het” are designed to measure proximities between entities in the first field given their cooccurrence distribution in the second field. They require two different fields (F₁ ≠ F₂) but produce homogeneous proximity networks with only entities of first field.

Heterogeneous cosine